9.3 Curvature and Components of Acceleration

Tangent Vector

$$\overrightarrow{T(t)}=\frac{\overrightarrow{r^{\prime }(t)}}{|\overrightarrow{r^{\prime }(t)}|}$$

 

$$\frac{d\overrightarrow{r}}{ds}=\frac{\frac{d\overrightarrow{r}}{dt}}{\frac{ds}{dt}}=\frac{\overrightarrow{r^{\prime }(t)}}{|\overrightarrow{r^{\prime }(t)}|}=\overrightarrow{T(t)}$$

---

Curvature

$$\kappa =|\frac{d\overrightarrow{T}}{ds}|=\frac{|\overrightarrow{T^{\prime }(t)}|}{|\overrightarrow{r^{\prime }(t)}|}$$

---

Acceleration

$$\overrightarrow{a(t)}=v\frac{d\overrightarrow{T}}{dt}+\frac{dv}{dt}\overrightarrow{T}$$

$$\overrightarrow{N(t)}=\frac{d\overrightarrow{T}/dt}{|d\overrightarrow{T}/dt|}$$

$\overrightarrow{a(t)}$는 Normal방향 가속과 Tangent방향 가속으로 분리할 수 있다.

$$\begin{array}{rl}\overrightarrow{a(t)}& =\kappa v^2\overrightarrow{N}+\frac{dv}{dt}\overrightarrow{T}\\ & =a_N\overrightarrow{N}+a_T\overrightarrow{T}\end{array}$$

---

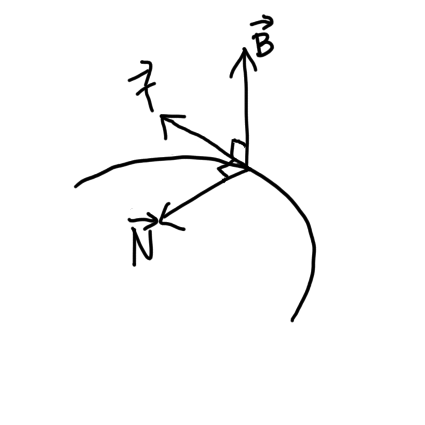
Binormal (TNB)

$\overrightarrow{T}$와 $\overrightarrow{N}$을 순서대로 외적하면 $\overrightarrow{B}$를 얻을 수 있다.

$$\begin{array}{rl}\overrightarrow{B(t)}& =\overrightarrow{T(t)}\times \overrightarrow{N(t)}\\ \overrightarrow{N(t)}& =\overrightarrow{B(t)}\times \overrightarrow{T(t)}\\ \overrightarrow{T(t)}& =\overrightarrow{N(t)}\times \overrightarrow{B(t)}\end{array}$$