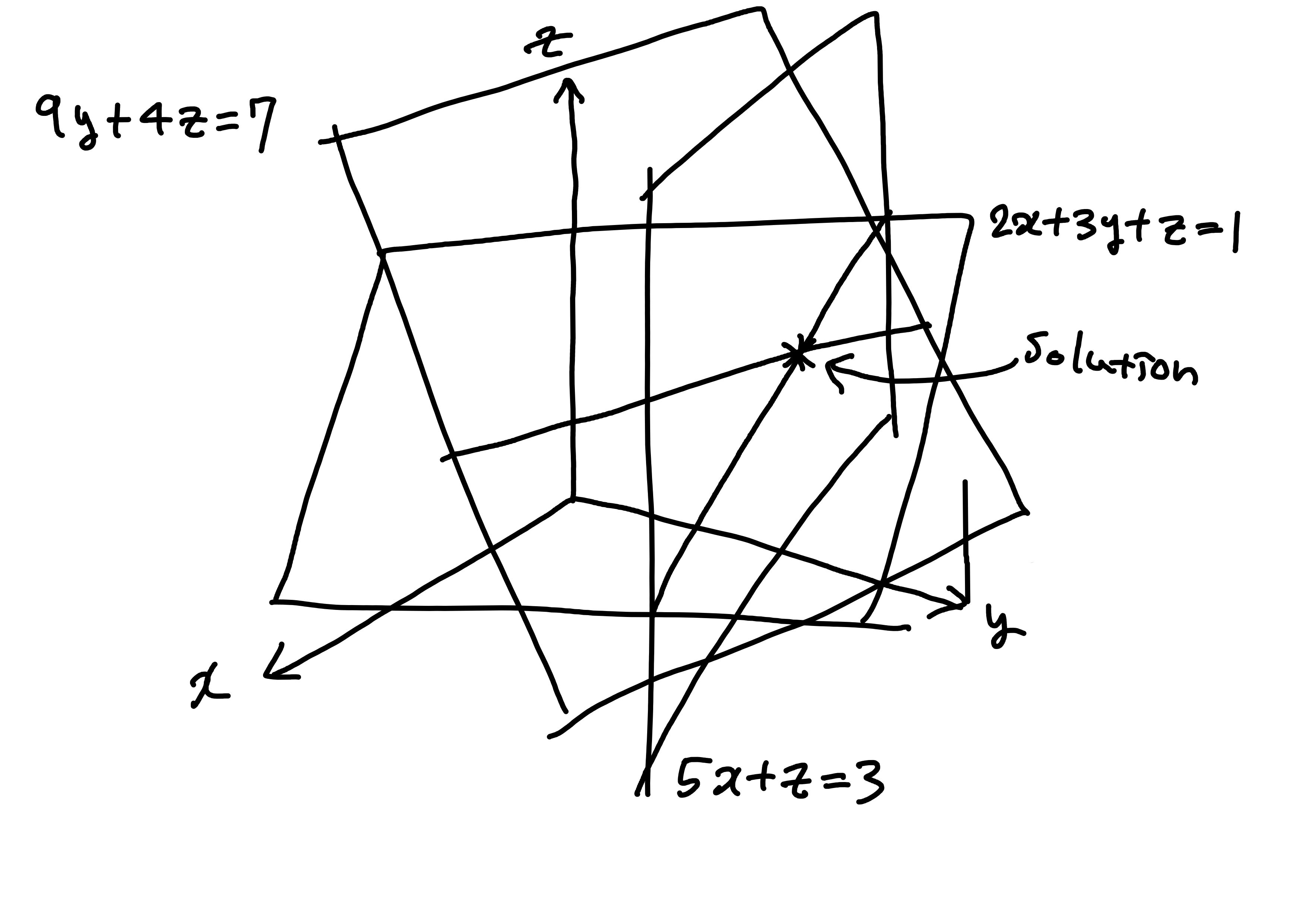
\[\begin{cases}2x+3y+z = 1 \\ 5x + z = 3 \\ 9y + 4z = 7 \end{cases}\]
위와 같은 선형연립방정식을 해석할 때 두 가지 관점이 있다.
Row concept
Column concept

Basic multiplication
Matrix에 multiplication을 할 때 Column기준이 있고 Row기준이 있다.
Column:
\[\left[\begin{array}{clr} 1& 2&3\\4&5&6\\7&8&9 \end{array}\right]\left[ \begin{array}{clr}x\\y\\z\\\end{array}\right] = x\left[\begin{array}{clr}1\\4\\7\end{array}\right] + y\left[\begin{array}{clr}2\\5\\8\end{array}\right] + z\left[\begin{array}{clr}3\\6\\9\end{array}\right]\]
Row:
\[\left[\begin{array}{clr}x & y & z \end{array}\right] \left[\begin{array}{clr} 1& 2&3\\4&5&6\\7&8&9 \end{array}\right] = \begin{array}{clr}x[\begin{array}{clr}1&2&3\end{array}]\\+\\y[\begin{array}{clr}4&5&6\end{array}]\\+\\z[\begin{array}{clr}7&8&9\end{array}]\end{array}\]
'기초수학 > 선형대수학' 카테고리의 다른 글
| Rank of an idempotent matrix is equal to the trace thereof (0) | 2023.12.25 |
|---|---|
| Eigenvalue, trace, determinant and rank of a matrix 간의 관계들 (0) | 2023.09.15 |
| 4. Vector Spaces (0) | 2023.01.11 |
| 3. Inverses and LU Factorization (0) | 2022.01.22 |
| 2. Gauss Elimination (0) | 2022.01.07 |